游戏编程：向量数学在游戏中如何使用

07月

340 0 0

文/崔

　　对于一个初学者来说，三维空间的几何似乎有点让人望而生畏。在纸上可以画出来的二维空间几何就已经足够难以理解了，但是现在我们竟然要使用和掌握三维空间的几何？

　　好消息是在图形学中直接使用三角形是非常罕见的并且有很多方法可以用来避免这么做。我们有其他更好理解和使用的工具来代替。你可能在下图中已经认出我们的老朋友-向量（vector）。

　　这篇文章将向你介绍三维空间的向量，并将用几个实际使用方面的例子来带你熟悉三维空间的向量。虽然这些例子的内容是侧重三维空间的，但是里面说明的大部分内容和原理也同样适用于二维空间。

　　这篇文章会假设读者具有代码和几何方面的知识，以及具有编程方面的经验和对面向对象编程(OOP)的基本了解。

　　游戏中的向量数学

　　概念

　　在数学中，一个向量是指一个既有方向（direction）又有大小(magnitue)的结构。在游戏开发中它经常用来描述位置的变化，并且可以与其他向量相加或者相减来得到新的位置变化（一个向量代表一个位置的变化，两个这样的向量相加得到的是这两段位置变化的总效果）。通常情况下，你会发现向量是数学库或者物理库的一部分。

　　它们通常包含一个或多个组件，比如x、y和z。向量可以是一维向量(只包含x分量)、二维向量(包含x、y分量)、三维向量(包含x、y、z分量)甚至是四维向量（一般是x、y、z、w分量）。四维向量可以用来描述其他一些东西，比如一个带额外alpha值的颜色。

　　对于初学者来说最困难的事情之一就是他们在刚接触向量的时候如何去理解看上去就是空间的一个点的东西为什么可以用来描述一个方向。

　　让我们用二维向量（3，3）来举例说明这个事情。要理解为什么向量能够代表一个方向你只需要看下面这张图。我们都知道需要两个点才能形成一条线。所以第二个点在哪里呢？缺失的那个点就是位于（0，0）的原点（origin）。我们画一条从原点（0，0）到（3，3）的线段，我们就得到下图这么一个效果：

　　正如你在上图中看到的那样，原点作为第二个点引入以后就与第一个点一起赋予了我们的向量一个方向。但是你也会看到，第一个点（3，3）可以被移动（或者说位移）来接近或者远离原点。

　　第一个点到原点的距离就被称为大小，可以用二次方程a^2 + b^2 = c^2计算得到。在我们举得例子中，就是3^2 + 3^2 =c^2， c = sqrt(18) ~= 4.24。如果我们把向量的每个分量除以4.24那么我们就把向量放缩成了大小正好为1（也就是到原点的距离为1）的向量。在接下来的例子中我们将看到为什么这个被称为向量归一化的过程非常有用，向量的归一化保留了向量的方向，但是提供了通过对数字（也就是标量)值进行乘法来放缩大小的能力。

　　在接下来的例子中，我将假设你的数学库用Vector2 代指二维向量，用Vector3代指三维向量。它们在不同的库和编程语言中有各种不同的名字，举个例子来说，vector、vector3、 Vector3f、 vec3、 point、 point3f等等都是向量的名字。你的数学库中关于向量部分肯定有很多文档和例子。

　　注意：向量类型在编程语言的世界里面通常有两种含义，既可以用来指传统的数学/物理场景中的向量，也可以用来表示自行控制的n维单位。这里仅仅是做一个小提醒。

　　像其他变量一样，你代码中的向量到底代表着什么含义完全取决于你的控制：它可以是一个位置、方向或者速度。下面是游戏中常见的一些向量用法

　　位置 - 向量代表着真实位置与你的世界坐标原点(0, 0, 0)的一个偏移量。

　　方向 - 向量看起来非常像是一个箭头指着某个方向。它确实是可以这么用。举个例子来说，如果你有一个指向南的向量，那么你可以把这个向量赋予你的所有单位作为它们的新方向，那么它们都将面向南。

　　方向向量的一个特例是长度为1的向量。它也被称为归一化的向量或者简称为标准向量。

　　一个速度（velocity ）向量可以描述一个运动。在这种情况下，它描述的是特定时间内的位置的变化。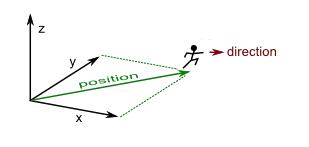

　　记住最基本的内容-向量加法和减法

　　向量加法是用来累加两个向量所描述的不同，并写入最后的向量中。

　　比如说，一个物体移动了A向量这么大的位移，然后又移动了Ｂ向量这么大的位移，那么结果就仿佛是它一共移动了Ｃ向量这么大的位移（其中C = A + B）。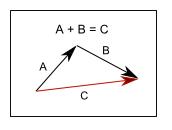

　　对于向量减法来说，就相当于把第二个向量反转，然后把反转的向量加到第一个向量身上。

　　注意：坐标系解向量加减法：

　　在直角坐标系里面,定义原点为向量的起点.两个向量和与差的坐标分别等于这两个向量相应坐标的和与差若向量的表示为(x,y)形式,

　　A(X1,Y1) B(X2,Y2)，则A+B=（X1+X2，Y1+Y2），A-B=（X1-X2，Y1-Y2）

　　简单地讲：向量的加减就是向量对应分量的加减。类似于物理的正交分解。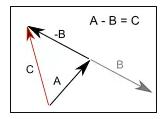

　　例子: 物体之间的距离

　　如果在这个例子中，向量代表的分别是物体A和B的位置，那么 B – A将是代表着A和B物体位置差的向量。 B – A所得到的结果将表示A位置移动到B位置所需的方向和距离。

　　举个例子来说，要得到人到树的距离向量你必须用树的位置减去人的位置，如下图所示：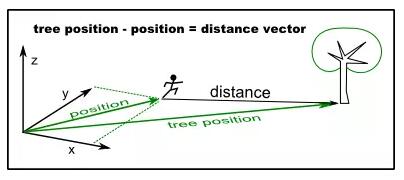

　　我用了伪代码（pseudo-code ）来保持代码的简洁方便阅读。在括号内的三个数字（x,y,z）代表着一个向量。：

　　注意：伪代码是一种算法描述语言。使用伪码的目的是使被描述的算法可以容易地以任何一种编程语言（Pascal，C，Java等）实现。因此，伪代码必须结构清晰、代码简单、可读性好，并且类似自然语言。介于自然语言与编程语言之间。以编程语言的书写形式指明算法职能。使用伪代码，不用拘泥于具体实现。相比程序语言（例如Java,C++,C, Dephi 等等）它更类似自然语言

　　tree_position = (10, 10, 0)

　　my_position = (3, 3, 0)

　　# distance anddirection you would need to move

　　# to getexactly where the tree is

　　vector_to_tree = tree_position - my_position

　　例子: 速度

　　除了位置向量以外，对象可能还有一个向量用来表示速度。

　　举个例子来说，大炮炮弹的速度向量描述的是它下一秒将要移动的距离。

　　当第一次被发射的时候，大炮炮弹可能具有如下这些属性：

　　position = (0, 10, 10) # position: 10units in Y and Z direction

　　velocity = (500, 0, 0) # initialmovement is 500 units in X direction over the next second

　　每秒钟要基于速度向量来更新一次炮弹的位置：

　　position += velocity # add velocityto position and update position

　　概念: 仿真

　　等等！我们不希望每一秒才更新一次物体。事实上，我们希望尽可能的频繁更新物体的信息。

　　但是我们不能指望两次更新之间的时间总是固定的。所以我们使用了delta时间，这是上一次更新到这一次更新的时间差。

　　因为delta时间代表的是逝去时间的一个时间差。所以我们可以用它来得到这次更新到上一次更新之间的这段时间内物体的移动速度所导致的位置差。

　　position += velocity * delta

　　这是一个非常基本的仿真。为了实现一个仿真，我们在自己的世界里面建模了我们的对象该具有怎样的行为（比如说大炮炮弹永远具有不变的速度）。然后我们加载最初的游戏状态（大炮炮弹开始的时候具有初始位置和速度）。

　　最后一块拼图是要把所有的东西融合在一起，这就是update循环，它会定期执行，我们用delta时间(也就是时间间隔)来记录上一次更新到这次更新的时间间隔。在每次update调用的时候，它会根据我们预先定义好的规则（比如说用炮弹的速度来更新炮弹的位置）来对每个仿真物体进行更新。

　　例子:重力、空气阻力和风

　　我们的炮弹移动是很无聊的：它永远是向一个方向移动并且移动的速度永远是不变的。我们需要它对周围的世界做出反应。举个例子来说，我们希望重力能让炮弹下落，希望空气阻力会让炮弹的速度变慢，至于风呢，仅仅是加进来为了好玩。

　　在一个游戏中重力实际上意味着什么呢?嗯，它会产生一个副作用，在物体向下的方向增加物体的速度。因为在我们的例子中Y轴是向上的，所以我们的重力向量将是下面这样的：

　　# increasevelocity of every object -2 down per second

　　gravity_vector = (0, -2, 0)

　　所以，在每次进行update调用之前，我们可以修改速度变量，如下面代码所示：

　　velocity += gravity_vector * delta # applygravity effect

　　position += velocity * delta # updateposition

　　让我们假设空气很厚，所以空气会每半秒就降低一次炮弹的速度。

　　velocity += gravity_vector * delta # applygravity effect

　　velocity *= 0.5 * delta # apply 0.5slowdown per second

　　position += velocity * delta # updateposition

　　速度会受到空气阻力的影响因为炮弹总是在空气中行进。空气会阻挡它的前进进而减少它的动能。所以我们需要调整下炮弹在空气中前进的速度。

　　但是，还有一个恒定的力会改变炮弹的运动，就像风一样

　　# modifykinetic energy / velocity

　　velocity += gravity_vector * delta # applygravity effect

　　velocity *= 0.5 * delta # apply 0.5slowdown per second

　　# add all forces

　　final_change_per_second = velocity + wind_force_per_second

　　# updateposition

　　position += final_change_per_second * delta

　　这个例子的着眼点在于说明用简单的向量数学构建如此复杂的一个行为是多么的容易。

　　概念: 方向

　　通常情况下，你不会需要从A到B的距离，而是需要从A指向B的方向。向量Ａ到向量B的距离当然可以用来表示方向，但是如果你需要从Ａ向B移动“很小一点点”，但是要精确的按照你希望的速度该怎样做呢？

　　在这种情况下向量长度应该无关紧要的，如果我们把方向向量的长度缩减为1，就可以用于这个目的以及其他一些情况。我们把这个缩减称为归一化（normalization ），得到的向量称为标准向量（normalvector）。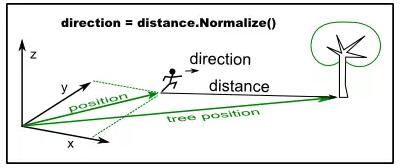

　　所以，一个标准向量它的长度应该总是1，否则它就不是一个标准向量。。

　　一个标准向量代表的是一个角度，而没有实际位置移动相关的其他任何信息。如果我们用一个标量数字乘以一个标准向量，我们就得到了一个方向向量，同时它的长度就是标量数字的大小。

　　在你的数学库里面应该有一个normalize函数，来从任意的向量中得到一个标准向量。

　　所以如果要朝B精确的移动3个单位长度，代码如下：

　　final_change = (B - A).normalize() * 3

　　概念：平面

　　一个标准向量也可以用来描述一个平面所朝向的方向。你可以把平面想象成从一个特定点P出发的无限大的片，对这个片的旋转可以通过法向量Ｎ来精确描述出来。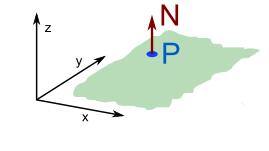

　　要旋转这个片／平面，你应该改变它的法向量。

　　注意：法向量是空间解析几何的一个概念，垂直于平面的直线所表示的向量为该平面的法向量。由于空间内有无数个直线垂直于已知平面，因此一个平面都存在无数个法向量（包括两个单位法向量）。如果一个非零向量n与平面a垂直，则称向量n为平面a的法向量。垂直于平面的直线所表示的向量为该平面的法向量。每一个平面存在无数个法向量。

　　概念: 点积(Dot Product)

　　点积是对两个向量进行操作然后返回一个数字。你可以把返回的这个数字看作是两个向量比较的一个方法。

　　注意：在数学中，点积（dot product; scalar product，也称为数量积）是接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。

　　通常写为：

　　result = A dot B

　　两个法向量之间的这种比较是特别有用的，因为这个数字会代表着他们在旋转上的不同。

　　如果点积返回的结果为1，说明这两个法向量指向同一个方向。

　　如果点积返回的结果为0，说明这两个法向量互相垂直。

　　如果点积返回的结果为-1，说明这两个法向量指向完全相反的方向。

　　下面这张图说明的是点积返回的结果与两个向量之间夹角的关系：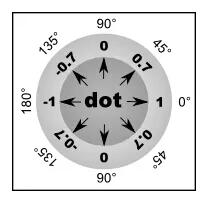

　　请注意上图中从1到0以及从0到-1的变化不是线性的，而是遵循余弦曲线进行变化的。所以，要从点积的结果中得到一个角度，你需要对返回的结果调用反余弦，如下面代码所示:

　　angle = acos(A dot B)

　　例子: 光照

　　试想一下我们正在写一个光照着色器并且我们需要计算一个特定表面点的像素明亮度。我们有如下这些信息：

　　一个法向量用来表示这个点上的表面的方向

　　光源的位置

　　这个表面点的位置

　　我们可以得到计算特定点到光源的距离向量:

　　distance_vec = light_pos - point_pos

　　以及把这个特定点上的光照方向变为一个标准向量：

　　light_direction = distance_vec.normalize()

　　然后基于我们已有的关于角度和点积（dot product）之间关系的知识，我们可以使用表面法向量和光照方向之间的点积来计算这个点的明亮度。在最简单的情况下，它就完全等于点积得到的结果!

　　brightness = surface_normaldot light_direction

　　不管你是否相信，这就是一个简单的光照着色器的基本框架。OpenGL中的实际片段着色器代码就是这样的（如果你没有着色器的相关知识也不用担心，这只是一个用来说明点积实际应用的例子，我们不会在着色器方面展开太多）:

　　注意：Shader(着色器)是用来实现图像渲染的用来替代固定渲染管线的可编辑程序。Shader分为Vertex Shader（顶点着色器）和Pixel Shader（像素着色器两种（（注：两种着色器在不同的实现中略有不同）。其中Vertex Shader主要负责顶点的几何关系等的运算，Pixel Shader主要负责片源颜色等的计算。

　　着色器替代了传统的固定渲染管线，可以实现3D图形学计算中的相关计算，由于其可编辑性，可以实现各种各样的图像效果而不用受显卡的固定渲染管线限制。这极大的提高了图像的画质。

　　varying vec3surface_normal;

　　varying vec3vertex_to_light_vector;

void main(void)
{
vec4diffuse_color = vec3(1.0, 1.0, 1.0); // the color of surface - white
float diffuse_term = dot(surface_normal, normalize(vertex_to_light_vector));
gl_FragColor = diffuse_color * diffuse_term;
}

　　dot1 = SN dot (SP - P1)

　　dot2 = SN dot (P2 - P1)

　　你可以计算它与平面相交的”程度“，也就是将这两个值相比较（相除）。

　　u = (SN dot (SP - P1)) / (SN dot (P2 - P1))

　　如果 u == 0，那么线段是与平面平行的。

　　如果 u <= 1 并且 u > 0，那么线段与平面相交。

　　如果u > 1，那么线段与平面不相交。

　　可以将线段的向量与u相乘得到精确的相交点：

　　intersectionpoint = (P2 - P1) * u

　　概念: 向量积（Cross Product）

　　向量积也是对两个向量的一个操作。结果是一个新的向量，它与前两个向量垂直，并且它长度是前两个向量长度的均值。

　　注意：向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量的和垂直。

　　两个向量a和b的叉积写作a×b（有时也被写成a∧b，避免和字母x混淆）。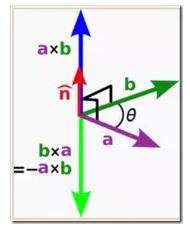

　　向量积可以被定义为：向量a×向量b=absinθ在这里θ表示两向量之间的夹角(共起点的前提下)（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。

　　需要注意的是对于向量积操作来说，参数的顺序是有影响的，如果调换了参数的顺序，生成的结果向量长度不变，但是方向将会完全相反。

　　例子: 碰撞

　　假设物体以某个角度往墙那里移动。但是墙是无摩擦的，所以物体应该沿着墙的表面移动而不是停下来。在这种情况下，如何计算物体的新位置？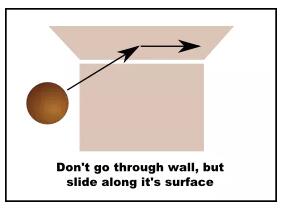

　　首先，我们用一个向量来表示如果没有墙的情况下物体应该移动的距离。我们将称它为“变化向量“。然后，我们将假设物体触碰到了墙。并且我们还需要墙表面的法向量。

　　我们将使用向量积来得到一个新的向量，它与”变化向量“和平面法向量相垂直：

　　temp_vector = change crossplane_normal

　　然后，最后的方向是与新的向量以及之前的平面法向量相垂直的：

　　new_direction = temp_vectorcross plane_normal

　　所以，就如下面代码这样得到最后的结果：

　　new_direction = (change crossplane_normal) cross plane_normal

　　现在该怎么办?

　　通过这篇文章，我希望能弥补向量数学的理论和在游戏开发中实际应用之间的鸿沟。但是，这也意味着我在讲解的过程中跳过了大量的东西。

　　但是我希望在阅读完这篇文章以后，你对向量数学的整体框架更加清楚一点。文中对向量数学的遍历可以视为游戏开发中使用向量数学的一个概述。

　　相关阅读：游戏编程实用技能：2D游戏中坐标转换

via：GAD

标签：魔兽开发经验爬坑游戏开发者开发技术游戏开发论坛

你还没有登录，请先登录或注册！

还没有人评论，欢迎说说您的想法！